Intel Threading Building Blocks
As the hardware engineers cram more and more cores into the processors, software engineers are left to ponder about how to best exploit these new capabilities. Intel offers an open source C++ library they call Threading Building Blocks (TBB). Akin to competing solutions (OpenMP, GCD, PPL), the library allows the developer to break up the computation into bite size pieces called tasks. A task also has a successor (or parent) task which makes it possible to express a relationship describing who should run before whom. The library runtime then takes care of scheduling the tasks onto the physical threads. It is, however, error prone and inconvenient to program using the tasks. Thankfully, much of the programming can be expressed via higher level abstractions (especially those involving fork-join parallelism). For example, parallel_for function allows for using multiple threads to execute the iterations of the loop. Another example is parallel_pipeline function which allows for expressing pipes-and-filters kind of parallelism.TBB also has a facility called a Flow Graph. Designed for those situations when it is best to express the concurrency as a directed graph of dependencies between message emitting nodes, Flow Graph stands almost like a separate library within the library. Let's take a look at an example from TBB's online reference. In this example, every node will print its name after it receives a completion message from the node that it depends on. Here's the dependency graph:
And the corresponding code:
#include <cstdio>
#include "tbb/flow_graph.h"
using namespace tbb::flow;
struct body {
std::string my_name;
body( const char *name ) : my_name(name) {}
void operator()( continue_msg ) const {
std::printf("%s\n", my_name.c_str());
}
};
int main() {
graph g;
broadcast_node< continue_msg > start;
continue_node<continue_msg> a( g, body("A"));
continue_node<continue_msg> b( g, body("B"));
continue_node<continue_msg> c( g, body("C"));
continue_node<continue_msg> d( g, body("D"));
continue_node<continue_msg> e( g, body("E"));
make_edge( start, a );
make_edge( start, b );
make_edge( a, c );
make_edge( b, c );
make_edge( c, d );
make_edge( a, e );
for (int i = 0; i < 3; ++i ) {
start.try_put( continue_msg() );
g.wait_for_all();
}
return 0;
}
The trouble with the code above is that the graph definition is not declarative. Looking at the series of make_edge calls, it is very hard to visualize the graph. I wanted to see if the situation could be improved...
Boost.Proto
I first encountered Boost.Proto at the Extraordinary C++ conference in 2007. Eric Niebler, the author of the library, gave a presentation to an awestruck audience where he took C++ metaprogramming to a level not seen before. In 2010, Eric wrote a series (1, 2, 3, 4, 5, 6, 7, 8) of articles on the subject that were published on C++Next blog. Through this wonderful series, I was finally able to start wrapping my head around Boost.Proto. The library is actually designed for library writers, more specifically those that are interested in developing an embeddable DSL inside C++ programs. I am not going try to give a tutorial of Boost.Proto in this post. If you have not yet done so, I highly recommend reading the aforementioned articles. What I hope to do is document my experience of using Boost.Proto for this exercise.Intel TBB meets Boost.Proto
To make the TBB's flow graph construction more declarative, let's create an EDSL for this task. Ideally the syntax would be as close to the picture of a graph as possible but that turned out to be difficult. Let's start with a simple case of few nodes in a row:
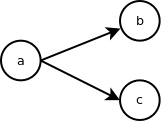
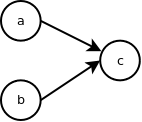
In the EDSL we will write this as a > b > c. Next, let's look at graphs where a node has more than one edge coming out of it or going into it:
We will write the left graph as a > (b + c) and the right one as (a + b) > c. Since when I see graphs like this, I tell to myself "a goes to b and c" and "a and b go to c", this syntax seems reasonable. And since in C++ the addition has higher precedence than greater operator, the parenthesis can be dropped: a > b + c and a + b > c. Let's use this syntax to express the graph in the original example: start > (a > e + c) + (b > c > d).
The Grammar
As I started working on defining a grammar for this mini language, I first defined it on paper using EBNF notation much like I would do if I was going to use yacc:expr ::= expr ">" group | group
group ::= group "+" node | "(" expr ")" | node
node ::= broadcast_node | continue_node
After a little fumbling however, I realized that Proto grammars can be much simpler. Since Proto expressions are C++ expressions, one does not have to worry about introducing parenthesis into the grammar nor trying to build operator precedence and associativity into it. Thus the grammar actually becomes:
expr ::= expr ">" expr
| expr "+" expr
| broadcast_node
| continue_node
A grammar like this would usually be ambiguous as it would be unclear how parse a > b > c, for example. But since C++ dictates the operator rules for us, there is no such ambiguity with Proto grammars! Written in Proto (transforms replaced with ellipses for now), it becomes:
namespace flow = tbb::flow;
namespace proto = boost::proto;
typedef flow::broadcast_node<flow::continue_msg> bcast_node;
typedef flow::continue_node<flow::continue_msg> cont_node;
typedef proto::literal<bcast_node> bcast;
typedef proto::literal<cont_node> cont;
struct grammar
: proto::or_<
proto::when<proto::plus<grammar, grammar>, ...>,
proto::when<proto::greater<grammar, grammar>, ...>,
proto::when<bcast, ...>,
proto::when<cont, ...>
>
{};
The Transforms
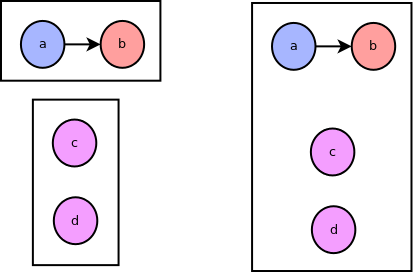
With the grammar in place, it's time to make it actually do stuff. We need to put in semantic actions, or transforms as Proto calls it, next to each grammar rule. In TBB, each node is both a sender and receiver of messages (and is derived from sender<T> and receiver<T>). As we combine the nodes together using the two operators, we produce a compound node which has some of the nodes inside of it acting as its senders and some as receivers. For example, suppose we have an expression (a > b) > (c > d > e) and we have independently build up two compound nodes, (a > b) and (c > d > e). We now join the two using the > operator. The > operator splices together the left-hand's senders with right-hand's receivers. In the diagrams below, the box represents the compound node, the receivers are colored blue, the senders are colored red and nodes acting as both receivers and senders are colored purple. For the example above, the following diagram illustrates the before and after the splice. Note that while 'a' is sending messages to 'b', it is actually the receiver of the compound node.The + operator joins the two compound nodes by combining the left-hand's receivers with right-hand's receivers and left-hand's senders with right-hand's senders. Again, suppose for the expression (a > b) + (c + d) we are joining (a > b) with (c + d). The following diagram shows the before and after:
Finally, let's go back to the > operator for the case when there are multiple senders being spliced to multiple receivers. In that case we splice each of the lefthand's senders to each of the right-hand's receivers. Thus, executing > operator on expressions (a + b) and (c + d + e) results in the following graph:
We now have all the pieces to start looking at code. Here are some typedefs:
typedef std::set<flow::sender<flow::continue_msg>*> sender_set;
typedef std::set<flow::receiver<flow::continue_msg>*> receiver_set;
typedef std::tuple<sender_set, receiver_set> compound_node;
Next up is the easiest of the transforms. When we encounter the terminals, broadcast_node or continue_node, we make a compound_node that only has that node inside of it:
struct make_compound_node : proto::callable
typedef compound_node result_type;
compound_node operator()(flow::sender<flow::continue_msg>& s, flow::receiver<flow::continue_msg>& r) {
return compound_node({&s}, {&r});
}
};
struct grammar
: proto::or_<
proto::when<proto::plus<grammar, grammar>, ...>,
proto::when<proto::greater<grammar, grammar>, ...>,
proto::when<bcast, make_compound_node(proto::_value, proto::_value)>,
proto::when<cont, make_compound_node(proto::_value, proto::_value)>
>
{};
Next, we take care of + operator. Remember, we just need to join the two senders' sets into one and do the same for the receivers' sets:
struct join : proto::callable {
typedef compound_node result_type;
compound_node operator()(compound_node left, compound_node right) const {
sender_set& senders = std::get<0>(left);
senders.insert(std::get<0>(right).begin(), std::get<0>(right).end());
receiver_set& receivers = std::get<1>(left);
receivers.insert(std::get<1>(right).begin(), std::get<1>(right).end());
return compound_node(std::move(senders), std::move(receivers));
};
};
struct grammar
: proto::or_<
proto::when<proto::plus<grammar, grammar>, join(grammar(proto::_left), grammar(proto::_right))>,
proto::when<proto::greater<grammar, grammar>, ...>,
proto::when<bcast, make_compound_node(proto::_value, proto::_value)>,
proto::when<cont, make_compound_node(proto::_value, proto::_value)>
>
{};
And finally the > operator:
struct splice : proto::callable {
typedef compound_node result_type;
compound_node operator()(compound_node left, compound_node right) const {
for( auto s: std::get<0>(left) )
for( auto r: std::get<1>(right) )
flow::make_edge(*s, *r);
sender_set& senders = std::get<0>(right);
receiver_set& receivers = std::get<1>(left);
return compound_node(std::move(senders), std::move(receivers));
}
};
struct grammar
: proto::or_<
proto::when<proto::plus<grammar, grammar>, join(grammar(proto::_left), grammar(proto::_right))>,
proto::when<proto::greater<grammar, grammar>, splice(grammar(proto::_left), grammar(proto::_right))>,
proto::when<bcast, make_compound_node(proto::_value, proto::_value)>,
proto::when<cont, make_compound_node(proto::_value, proto::_value)>
>
{};The only thing that is left is main() demonstrating the usage:
int main() {
flow::graph g;
bcast start(g);
cont a = cont_node( g, body("A"));
cont b = cont_node( g, body("B"));
cont c = cont_node( g, body("C"));
cont d = cont_node( g, body("D"));
cont e = cont_node( g, body("E"));
auto expr =
start > (a > e + c)
+ (b > c > d);
grammar()(expr);
proto::value(start).try_put( flow::continue_msg() );
g.wait_for_all();
return 0;
}
A big thanks goes to Neil Groves for reviewing this article.